4.2.2 Polinomios de interpolacion de lagrange

POLINOMIOS DE INTERPOLACION DE LAGRANGE

Empezamos con un conjunto de n+1 puntos en el plano (que tengan diferentes coordenadas x):
(x0, y0), (x1, y1), (x2, y2),....,(xn, yn).

Nuestro objetivo es encontrar una función polinómica que pase por esos n+1 puntos y que tengan el menor grado posible. Un polinomio que pase por varios puntos determinados se llama un polinomio de interpolación.

Vamos a ver una forma de la solución que es el llamado polinomio de interpolación de Lagrange. (Lagrange publicó su fórmula en 1795 pero ya había sido publicada en 1779 por Waring y redescubierta por Euler en 1783).

La fórmula general para el polinomio de interpolación de Lagrange es
Donde usamos polinomios básicos de Lagrange: 
Expandiendo el producto para verlo mejor:

POLINOMIOS DE INTERPOLACION DE LAGRANGE EN MATLAB

del polinomio de Lagrange en MATLAB, podemos emplear la funcion 'poly' construida con este
proposito, la que construye un polinomio dadas sus raices. Por ejemplo, tecleamos lo siguiente para construir un polinomio con raices x = 1 y x = 2:



ans = 1 -3 2

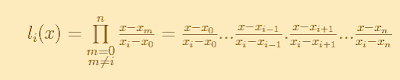
Comentarios

Publicar un comentario

Entradas populares de este blog

4.1.2 Método de mínimos cuadrados

Imagen
MÉTODO DE MÍNIMOS CUADRADOS  El método de mínimos cuadrados sirve para interpolar valores, dicho en otras palabras, se usa para buscar valores desconocidos usando como referencia otras muestras del mismo evento. El método consiste en acercar una línea o una curva, según se escoja, lo más posible a los puntos determinados por la coordenadas [x, f(x)], que normalmente corresponden a muestras de algún experimento. Cabe aclarar que este método, aunque es sencillo de implantar no es del todo preciso, pero si proporciona una interpolación aceptable. Como se comento previamente se puede usar una recta o una curva como base para calcular nuevos valores. A continuación se muestra el diagrama de flujo de datos del métodos de mínimos cuadrados: Algoritmo en MATLAB para la aproximación lineal por el método de los mínimos cuadrados. El siguiente algoritmo recibe un número arbitrario de pares de datos en la forma de una matriz de 2*n, donde las abcisas se encuentran en la ...
Leer más

4.2.1 Polinomio de interpolacion con diferencias divididas de newton

POLINOMIO DE INTERPOLACION CON DIFERENCIAS DIVIDIDAS DE NEWTON En  análisis numérico , la  interpolación polinómica  es una técnica de  interpolación  de un conjunto de datos o de una función por un  polinomio . Es decir, dado cierto número de puntos obtenidos por  muestreo  o a partir de un  experimento  se pretende encontrar un polinomio que pase por todos los puntos. Dada una función  f  de la cual se conocen sus valores en un número finito de abscisas  x 0 , x 1 ,..., x m , se llama  interpolación polinómica  al proceso de hallar un  polinomio   p m ( x ) de grado menor o igual a m. Motivación del polinomio interpolador La interpolación polinómica es un método usado para conocer, de un modo aproximado, los valores que toma cierta función de la cual sólo se conoce su imagen en un número finito de  abscisas . A menudo, ni siquiera se conocerá la expresión de la función ...
Leer más

4.1.2.3 Regresión lineal multiple

Imagen
REGRESIÓN LINEAL MÚLTIPLE El modelo de regresión lineal múltiple es idéntico al modelo de regresión lineal simple, con la única diferencia de que aparecen más variables explicativas:  Modelo de regresión simple:  y = b0+ b1 ⋅ x + u   Modelo de regresión múltiple:  y =b 0 + b1 ⋅ x1 +b 2 ⋅ x2 + b3 ⋅ x3 + ... + bk ⋅ xk + u Siguiendo con nuestro ejemplo, si consideramos el peso como variable dependiente y como posibles variables explicativas:  estatura  ƒ pie  ƒ l_brazo  ƒ a_espalda  ƒ d_craneo  El modelo que deseamos construir es:  peso = b0+b1* estatura+b2*pie+b3*1_brazo+b4*a_espalda+b5*d_craneo Al igual que en regresión lineal simple, los coeficientes b van a indicar el incremento en el peso por el incremento unitario de la correspondiente variable explicativa. Por lo tanto, estos coeficientes van a tener las correspondientes unidades de medida. REGRESIÓN LINEAL MÚLTIPLE EN MATLAB En el siguiente...
Leer más